What is a Neural Network?
A neural network is a computational model inspired by the structure and function of the human brain. It consists of interconnected nodes, or artificial neurons, organized in layers that process information to solve complex problems like image recognition, natural language processing, and predictive modeling. The fundamental operation of a neural network involves receiving inputs, processing them through various layers, and producing outputs based on learned patterns.
Structure of Neural Networks
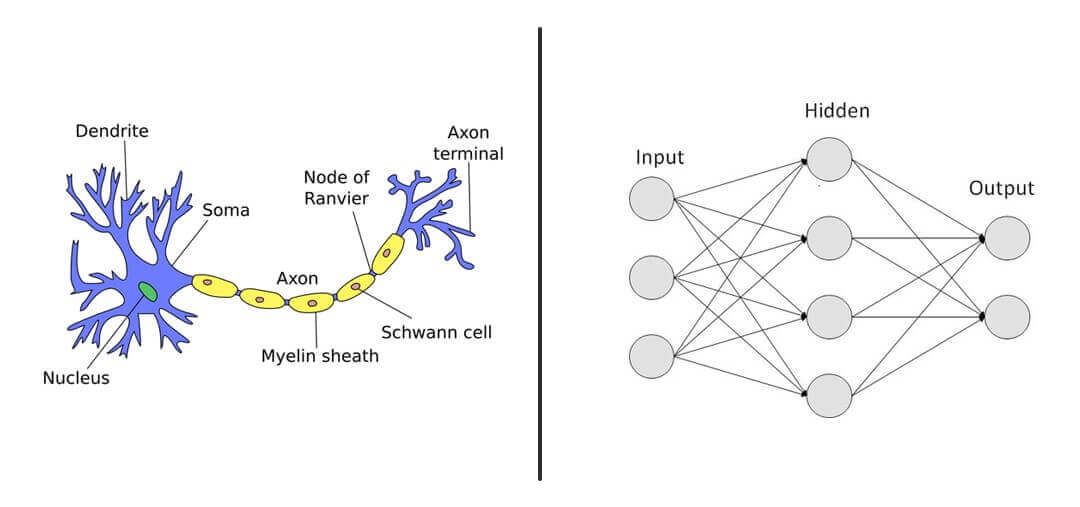
Layers
Neural networks typically consist of three main types of layers:
Input Layer: This is the first layer that receives raw input data. Each neuron in this layer represents a feature of the input data.
Hidden Layers: These layers are between the input and output layers. They perform computations and transform the input into something the network can use. A neural network can have one or more hidden layers, which allow it to learn complex representations.
Output Layer: This is the final layer that produces the output of the network, such as classification results or predictions.
Neurons and Connections
Each neuron in a neural network mimics biological neurons in the human brain. Neurons receive inputs through connections (analogous to synapses) from other neurons. Each connection has an associated weight that signifies its strength. During training, these weights are adjusted through a process called backpropagation, which minimizes the error between the predicted output and the actual output.
Types of Neural Networks
Neural networks can be categorized based on their architecture and application:
Feedforward Neural Networks (FNN): Information moves in one direction—from input to output—without cycles or loops. This is the simplest type of neural network.
Convolutional Neural Networks (CNN): Primarily used for image processing, CNNs utilize convolutional layers to automatically detect features in images.
Recurrent Neural Networks (RNN): These networks are designed for sequential data processing, allowing connections between nodes to form cycles. They are particularly useful for tasks like language modeling and time series prediction.
Autoencoders: These are used for unsupervised learning tasks like dimensionality reduction. They consist of an encoder that compresses data and a decoder that reconstructs it.
Long Short-Term Memory Networks (LSTM): A type of RNN that can learn long-term dependencies, effectively handling sequences with varying time delays.
Spiking Neural Networks (SNN): These networks incorporate time into their computations, processing information as discrete events (spikes), similar to how biological neurons operate.
Biological Analogy

The structure of artificial neural networks draws parallels with biological neural systems:
Neurons: In both systems, neurons receive signals from other neurons through connections. In biological systems, these connections are synapses.
Axons: In biological neurons, axons transmit signals away from the neuron. Similarly, in a neural network, outputs from one layer serve as inputs to the next layer.
Synapses: The strength of connections in both biological and artificial networks can change over time. In artificial networks, this is done through training algorithms that adjust weights based on error feedback.
In summary, neural networks are powerful tools modeled after human brain functions, capable of learning complex patterns through layered architectures and interconnected nodes. Their diverse types cater to various applications across fields such as computer vision, natural language processing, and more.
Certainly! Here’s a refined version without numbered points:
Components of a Perceptron

A perceptron consists of several key components:
Input Layer: This includes one or more input neurons that receive signals from the external environment or other layers in the network.
Weights: Each input is associated with a weight, which signifies the strength of the connection between the input neuron and the output neuron. These weights determine how much influence each input has on the output.
Bias: A bias term is added to the weighted sum of inputs to provide additional flexibility in modeling complex patterns. It allows the model to adjust the decision boundary independently of the input values.
Activation Function: This function determines the output based on the weighted sum of inputs plus the bias. Common activation functions include:
Step Function: Outputs 1 if the input exceeds a certain threshold, otherwise outputs 0.
Sigmoid Function: Outputs values between 0 and 1, useful for probabilistic interpretations.
ReLU (Rectified Linear Unit): Outputs zero for negative inputs and passes positive inputs unchanged.
Output: The final output of a perceptron is typically a binary value (0 or 1), indicating class membership based on the input data.
How Perceptrons Work
The operation of a perceptron can be summarized as follows:
First, it calculates a weighted sum of its inputs, combining them with their respective weights and adding a bias term. This calculation produces a value that is then passed through an activation function to generate the final output.
During training, perceptrons adjust their weights based on errors in predictions using techniques such as gradient descent. The learning rule updates weights to minimize error between predicted and actual outputs.
Limitations and Extensions
While single-layer perceptrons are effective for linearly separable problems, they have limitations and cannot solve problems that are not linearly separable (e.g., XOR problem). To address these limitations, multi-layer perceptrons (MLPs) were developed. MLPs consist of multiple layers of neurons, allowing them to learn complex patterns by stacking several layers of perceptrons. This architecture enables them to handle non-linear relationships in data effectively.
Importance in Neural Networks
Understanding perceptrons is vital because they form the building blocks of more complex neural networks. Their ability to model simple decision boundaries lays the groundwork for understanding how larger networks can learn intricate patterns across various applications such as image recognition, natural language processing, and more.
In summary, perceptrons encapsulate fundamental principles that underpin modern neural networks, making them crucial for anyone interested in machine learning and artificial intelligence.
What is a Feed-Forward Neural Network?
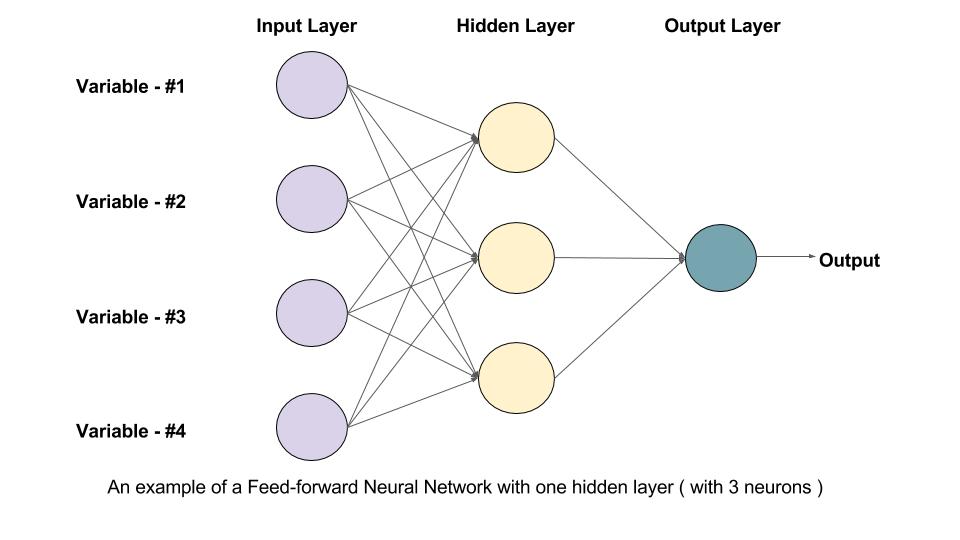
A Feed-Forward Neural Network (FFNN) is the simplest form of artificial neural networks. It consists of layers of neurons where information moves in only one direction—forward—from the input layer, through hidden layers, to the output layer. There are no cycles or loops, hence the term "feed-forward."
Key Characteristics
Unidirectional Data Flow: In a feed-forward network, data flows from the input layer to the output layer without looping back.
Layer Structure: Typically comprises an input layer, one or more hidden layers, and an output layer.
Activation Functions: Neurons in the hidden layers apply activation functions (like ReLU, Sigmoid, or Tanh) to introduce non-linearity.
Output Generation: The final output layer produces a prediction or classification based on the weighted sum of inputs.
Applications
Feed-Forward Neural Networks are commonly used in:
Classification tasks (e.g., image recognition)
Regression analysis
Pattern recognition
Time series prediction
What is Back-Propagation?
Overview
Back-Propagation is a supervised learning algorithm used for training neural networks. It is not a type of neural network but rather a method used to optimize the weights of the connections between neurons. Back-propagation works by minimizing the error between the actual output and the predicted output of the neural network.
Key Characteristics
Error Calculation: During training, the network's output is compared with the actual target, and the difference (error) is calculated.
Gradient Descent: Back-propagation utilizes gradient descent to adjust the weights of the network by calculating the gradient of the error with respect to each weight.
Reverse Data Flow: Unlike feed-forward, back-propagation involves data moving backward—from the output layer to the input layer—to update weights and minimize the error.
Iterative Process: The process is repeated over many iterations (epochs) until the network's output error is minimized to an acceptable level.
Applications
Back-Propagation is critical in:
Training deep neural networks
Fine-tuning the model to improve accuracy
Reducing overfitting and underfitting in models
What is an Activation Function?
An activation function is a mathematical function applied to the output of a neuron. It introduces non-linearity into the model, allowing the network to learn and represent complex patterns in the data. Without this non-linearity feature, a neural network would behave like a linear regression model, no matter how many layers it has.
Activation function decides whether a neuron should be activated by calculating the weighted sum of inputs and adding a bias term. This helps the model make complex decisions and predictions by introducing non-linearities to the output of each neuron.
Types of Activation Functions in Deep Learning
1. Linear Activation Function
Linear Activation Function resembles straight line define by y=x. No matter how many layers the neural network contains, if they all use linear activation functions, the output is a linear combination of the input.
The range of the output spans from (−∞ to +∞)(−∞ to +∞).
Linear activation function is used at just one place i.e. output layer.
Using linear activation across all layers makes the network’s ability to learn complex patterns limited.
Linear activation functions are useful for specific tasks but must be combined with non-linear functions to enhance the neural network’s learning and predictive capabilities.

2. Non-Linear Activation Functions
1. Sigmoid Function
Sigmoid Activation Function is characterized by ‘S’ shape. It is mathematically defined asA=1/1+e^-x. This formula ensures a smooth and continuous output that is essential for gradient-based optimization methods.
It allows neural networks to handle and model complex patterns that linear equations cannot.
The output ranges between 0 and 1, hence useful for binary classification.
The function exhibits a steep gradient when x values are between -2 and 2. This sensitivity means that small changes in input x can cause significant changes in output y, which is critical during the training process.

2. Tanh Activation Function
Tanh function (hyperbolic tangent function), is a shifted version of the sigmoid, allowing it to stretch across the y-axis. It is defined as:
Value Range: Outputs values from -1 to +1.
Non-linear: Enables modeling of complex data patterns.
Use in Hidden Layers: Commonly used in hidden layers due to its zero-centered output, facilitating easier learning for subsequent layers.
Understanding Neural Networks and Deep Learning
Neural networks and deep learning are pivotal in the evolution of artificial intelligence, enabling machines to learn from data similarly to how humans do. This blog explores foundational concepts, training methodologies, architectures, and the mathematical principles underlying these technologies.
The Biological Neuron and the Perceptron
At the core of neural networks is the concept of the biological neuron, which serves as a model for artificial neurons. A biological neuron receives input signals through dendrites, processes them in the cell body, and transmits output through axons.
The Perceptron, introduced by Frank Rosenblatt in 1958, is the simplest form of a neural network. It consists of a single layer of output nodes connected to input features. The Perceptron functions by applying weights to inputs and passing the weighted sum through an activation function to produce binary outputs.
Multilayer Feed-Forward Networks

Building on the Perceptron, Multilayer Feed-Forward Networks (MLPs) incorporate one or more hidden layers between input and output layers. Each neuron in these layers applies a transformation to its inputs, allowing MLPs to learn complex patterns in data. The architecture typically includes:
Input Layer: Receives input data.
Hidden Layers: Perform computations and feature extraction.
Output Layer: Produces final predictions.
Training Neural Networks
The training of neural networks primarily involves backpropagation, a supervised learning algorithm that adjusts weights based on the error between predicted and actual outputs. This process consists of:
Forward Propagation: Inputs are passed through the network to generate predictions.
Loss Calculation: A loss function quantifies the error of predictions.
Backward Propagation: The algorithm computes gradients of the loss function with respect to each weight and updates them accordingly.
Loss Functions
Loss functions measure how well a neural network's predictions align with actual outcomes. Different types are used depending on the task:
Regression Loss Functions: Mean Squared Error (MSE) is commonly used for continuous outputs.
Classification Loss Functions: Cross-Entropy Loss is prevalent for categorical outputs.
Reconstruction Loss Functions: Used in models like autoencoders to assess how well they reconstruct input data.
Hyperparameters
Hyperparameters are crucial settings that influence training dynamics:
Learning Rate: Determines step size during weight updates; too high may lead to divergence, while too low can slow convergence.
Regularization: Techniques like L1 and L2 regularization prevent overfitting by penalizing large weights.
Momentum: Accelerates convergence by considering past gradients.
Sparsity: Encourages models to maintain fewer active neurons, enhancing interpretability.
Fundamentals of Deep Networks
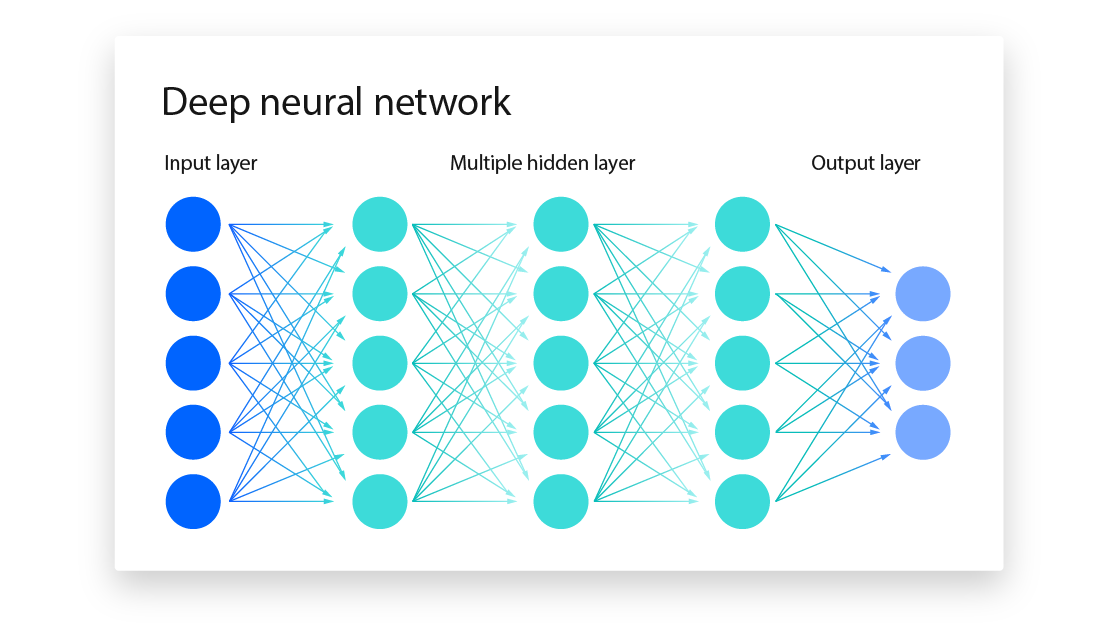
Deep learning extends traditional neural networks by adding multiple layers, allowing for hierarchical feature extraction. Key concepts include:
Mathematical Building Blocks
Deep networks rely on tensor operations for efficient computation across multiple dimensions. Tensors represent data in various forms (scalars, vectors, matrices), facilitating operations like matrix multiplication essential for neural computations.
Gradient-Based Optimization
Gradient descent is a foundational algorithm used to minimize loss functions by iteratively updating weights based on gradients calculated from training data.
Introduction to Keras and TensorFlow
Keras and TensorFlow are popular frameworks that simplify building and training deep learning models. Keras provides a user-friendly API for constructing networks, while TensorFlow offers robust tools for optimization and deployment.
Major Architectures of Deep Networks
Several architectures have emerged within deep learning, each tailored for specific tasks:
Unsupervised Pretrained Networks
These networks leverage unsupervised learning techniques to pretrain models before fine-tuning them on labeled datasets. Examples include:
Generative Adversarial Networks (GANs): Consist of two competing networks (generator and discriminator) that enhance each other's performance through adversarial training.
Deep Belief Networks (DBNs): Stack multiple layers of stochastic, latent variables that learn hierarchical representations of data.
Convolutional Neural Networks (CNNs)
CNNs are designed specifically for processing grid-like data such as images. They utilize convolutional layers that apply filters to capture spatial hierarchies in visual inputs. Key components include:
Input Layers: Accept image data.
Convolutional Layers: Extract features using filters that slide across input images.
CNNs have revolutionized fields like image recognition and computer vision due to their efficiency in handling high-dimensional data.
Neural networks and deep learning represent a significant advancement in artificial intelligence, mimicking human cognitive processes through structured architectures and sophisticated training methodologies. As these technologies continue to evolve, their applications will expand across various domains, including healthcare, finance, and autonomous systems. Understanding their fundamentals is crucial for anyone looking to navigate the landscape of modern AI effectively.
