Finite Automata
Definition of Finite Automata
Finite automata (FA) are simple computational models used to recognize patterns in input strings. They consist of a finite number of states and transition between these states based on input symbols.
The formal definition of a finite automaton is a 5-tuple (Q, Sigma, q_0, A, delta), where:
Q is a finite set of states.
Sigma is a finite input alphabet (the set of symbols the automaton can read).
q_0 is the initial state (where the automaton starts).
A is the set of accepting states (where the automaton can end successfully).
delta is the transition function that defines how the automaton moves from one state to another based on input symbols.
Language
Definition and Justification
A language in computer science refers to a set of strings formed from a specific alphabet. The statement "A language can be finite or infinite" means that:
Finite Language: Contains a limited number of strings.
For example, the language consisting of the strings {"cat", "dog", "fish"} is finite because it has only three strings.
Infinite Language: Contains an endless number of strings.
For instance, the language of all binary strings (combinations of 0s and 1s) is infinite because you can keep adding more digits indefinitely.
Deterministic Finite Automaton (DFA)
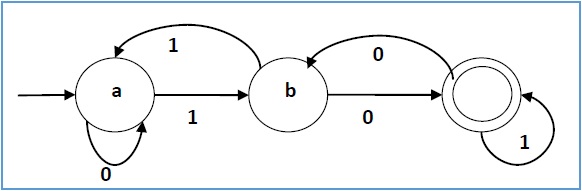
Definition and Example
A DFA is a type of finite automaton where for each state and input symbol, there is exactly one transition to another state. This means that given any input, the next state is uniquely determined.
An example of a DFA could be one that accepts binary strings ending with '0'. The states might be:
State q_0: Start state.
State q_1: Accepting state for strings ending in '0'.
State q_2: Rejecting state for strings ending in '1'.
The transitions would be:
From q_0 on '0' go to q_1.
From q_0on '1' go to q_2.
From q_1 on '0' stay in q_1; on '1' go to q_2.
From q_2, any input stays in q_2.
String Acceptance vs. Language Acceptance
String acceptance refers to whether a specific string is accepted by the finite automaton, meaning it ends in an accepting state after processing all its symbols. Language acceptance refers to the overall capability of the finite automaton to accept any string from a defined set or language. Thus, while string acceptance looks at individual cases, language acceptance considers all possible strings within that language.
Non-deterministic Finite Automaton (NFA)

Definition and Example
An NFA allows multiple transitions for the same input symbol from a given state and can also include transitions without consuming any input (ε-transitions). For example, consider an NFA that accepts strings containing at least one 'a':
States: q_0(start), q_1 (accept).
Transitions:
From q_0 on 'a' go to q_1.
From q_0 on 'b' stay in q_0.
From q_1, any input stays in q_1.
Differences Between NFA and DFA

The main differences between NFAs and DFAs are:
Determinism: DFAs have exactly one transition for each symbol from each state; NFAs can have multiple transitions or none.
State Complexity: NFAs can be more compact than DFAs since they can use fewer states for certain languages.
Acceptance Conditions: A string is accepted by an NFA if there exists at least one path through the states that leads to an accepting state.
ε-NFA
An ε-NFA (epsilon-NFA) is a type of NFA that allows transitions without consuming any input symbol. This means it can move from one state to another just by making an ε-transition, which does not require an input character.
Moore Machine vs. Mealy Machine
Moore Machine
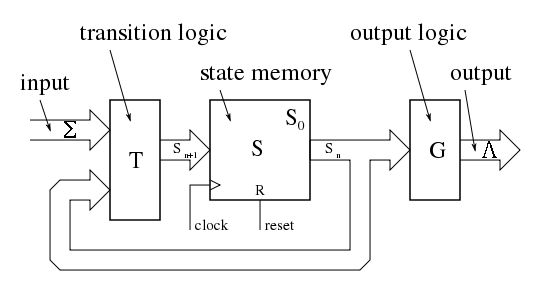
A Moore machine is a type of finite state machine where the output depends only on the current state. For example:
States: S1 (output = 0), S2 (output = 1).
Transition: On input 'a', move from S1 to S2; output changes based on the current state.
Mealy Machine
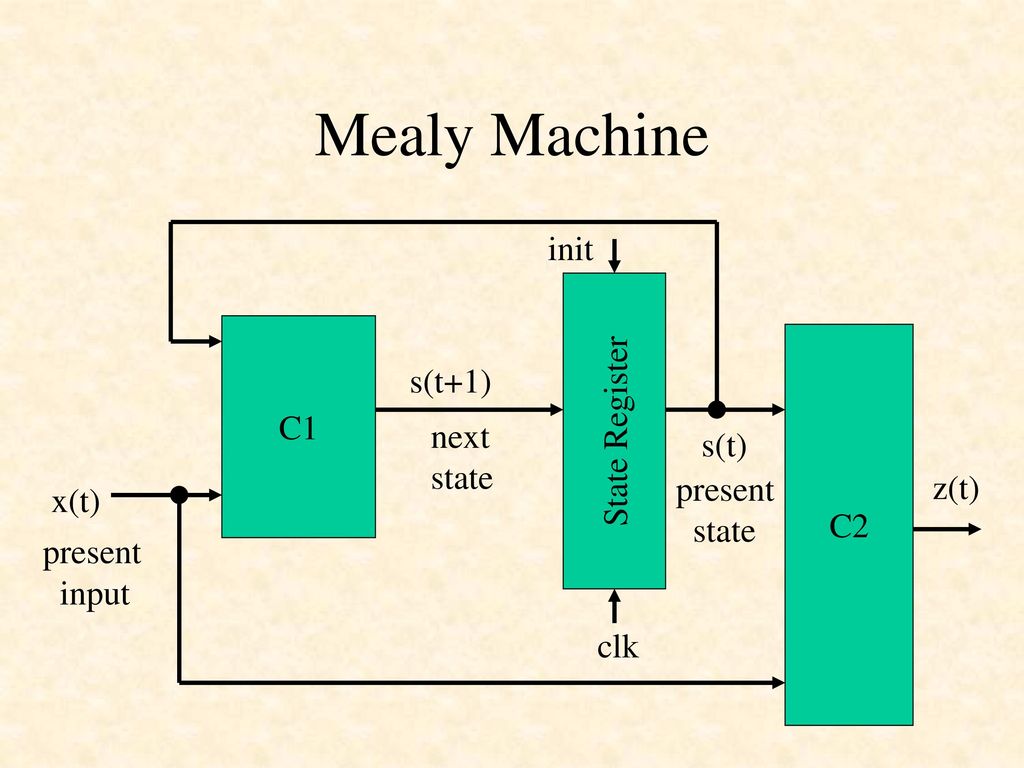
In contrast, a Mealy machine's output depends on both the current state and the current input. For example:
States: S1, S2.
Transition: On input 'a', move from S1 to S2 and output '1'; on input 'b', stay in S1 and output '0'.
Grammar
Definition and Example
Grammar defines how strings in a language can be formed using rules. The formal definition includes:
A set of variables (non-terminal symbols),
A set of terminals (actual symbols),
A start symbol,
A set of production rules that describe how variables can be replaced with combinations of variables and terminals.
For example, a simple grammar for arithmetic expressions might include:
Variables: E (expression), T (term), F (factor)
Terminals: +, *, (, ), id
Productions:
E → E + T
E → T
T → T * F
T → F
F → (E)
F → id
Chomsky Hierarchy

The Chomsky hierarchy classifies languages into four types based on their generative power:
Type 0: Recursively enumerable languages generated by unrestricted grammars.
Type 1: Context-sensitive languages generated by context-sensitive grammars.
Type 2: Context-free languages generated by context-free grammars.
Type 3: Regular languages generated by regular grammars.
Regular Grammar
Regular grammar is a type of formal grammar that generates regular languages. It consists of production rules where each rule replaces a variable with either a terminal followed by another variable or just a terminal.
Differences Between Regular Grammar, Regular Language, and Regular Expressions
Regular Grammar: A set of rules defining how to form strings in a regular language.
Regular Language: A collection of strings defined by regular grammar or recognized by finite automata.
Regular Expressions: A notation used to describe regular languages using patterns.
Pumping Lemma for Regular Languages
The pumping lemma states that for any regular language, there exists a length p such that any string longer than this length can be divided into three parts, xyz, satisfying certain conditions allowing repetition of part y. This property helps prove whether certain languages are not regular.
Closure Properties of Regular Sets
Closure properties refer to how certain operations on regular languages yield new regular languages. Examples include:
Union: The union of two regular languages is also regular.
Intersection: The intersection of two regular languages remains regular. For instance, if L1 = {a, ab} and L2 = {b}, then L1 ∪ L2 = {a, ab, b} which is also regular.
Context-Free Grammar (CFG)
A context-free grammar consists of production rules where each rule replaces a single variable with a string of variables and terminals. It generates context-free languages used in programming languages and compilers.
Comparison Between Context-Free Grammar and Regular Grammar
While both define languages:
CFGs can represent more complex structures than regular grammars because they allow nested patterns.
Regular grammars cannot express certain constructs like balanced parentheses which CFGs can easily handle.
Ambiguity in Grammar
Ambiguity occurs when a string can be generated by more than one distinct parse tree or derivation sequence in a grammar. For example, consider the grammar with productions:
S → AB
S → BA
A → 'a'
B → 'b'
The string "ab" can be derived as either "AB" or "BA", leading to ambiguity.
Chomsky Normal Form (CNF)
Chomsky Normal Form is a specific way to express context-free grammars where every production rule must either produce two non-terminal symbols or one terminal symbol. This format simplifies parsing algorithms.
Pushdown Automata (PDA)
A PDA extends finite automata with an additional stack memory structure allowing it to recognize context-free languages. It processes input symbols while manipulating its stack according to defined transitions.
Formal Definition of PDA
A PDA is formally defined as a 7-tuple (Q,Σ,Γ,q0,Z0,F,δ):
Q: Set of states,
Σ: Input alphabet,
Γ: Stack alphabet,
q0: Initial state,
Z0: Initial stack symbol,
F: Set of accepting states,
δ: Transition function defining how states change based on inputs and stack contents.
Closure Properties of Context-Free Languages (CFL)
Similar to regular languages, CFLs have closure properties but are more limited:
- CFLs are closed under union and concatenation but not under intersection or complementation.
Pumping Lemma for CFL
The pumping lemma for context-free languages asserts that for any context-free language, there exists some length such that any sufficiently long string can be split into parts allowing repetition while still remaining within the language.
Context-Sensitive Grammar
Context-sensitive grammar allows productions where variables can only be replaced if they are within specific contexts in strings. This type generates context-sensitive languages which are more powerful than context-free languages.
Unrestricted Grammar
Unrestricted grammar has no restrictions on its production rules and can generate recursively enumerable languages. These grammars are powerful enough to describe any computation that can be performed by Turing machines.
Turing Machine
A Turing machine is an abstract computational model capable of simulating any algorithmic process through its tape-based memory system and set transition rules defining its operations based on current states and tape symbols.
Formal Definition of Turing Machine
A Turing machine consists of:
A tape divided into cells containing symbols from an alphabet,
A head that reads/writes symbols on the tape,
A finite set of states including an initial state and one or more accepting states,
A transition function dictating how the machine moves between states based on read symbols.
Linear Bounded Automaton (LBA)
An LBA is a restricted type of Turing machine whose tape length is linearly bounded by the length of its input string. It recognizes context-sensitive languages.
Multi-Tape Turing Machine
This variant has multiple tapes allowing simultaneous reading/writing operations across different tapes which increases computational efficiency compared to single-tape machines.
Deterministic vs Non-deterministic Turing Machines
Deterministic Turing machines have exactly one action for each combination of state and tape symbol while non-deterministic machines may have multiple possible actions leading them down different computational paths simultaneously.
Recursive vs Recursively Enumerable Languages
Recursive languages are those for which there exists a Turing machine that will always halt with an answer (accept/reject). Recursively enumerable languages may not halt for some inputs but will accept valid inputs if they do halt; thus they encompass all recursive languages but also include some non-recursive ones as well.
